Hora oficial, legal, solar, canónica, etc.
Tabla de hora oficial, legal, UTC, civil, solar, sidérea, itálica, babilónica, temporaria, canónica y de otros datos solares
Nota 1: Los valores de la latitud y longitud que se utilizan en la tabla puede Ud. cambiarlos por los de otra localización. Los que se muestran inicialmente son los del Observatorio Astronómico (latitud 40.408333º Norte, longitud -3.687778º Este (40º 24' 30'', -3º 41' 16''), altitud 655 m) de Madrid, España. Fue la longitud de este Observatorio la que se utilizó como referencia geográfica-geodésica en España hasta que se sustituyó por la del meridiano de Greenwich, Reino Unido, a finales del siglo XIX y principios del XX.
Nota 2: Para que este applet funcione es necesario que su navegador lo permita. Asegúrese de que el reloj de su ordenador tiene la fecha y hora correctas. Se utilizan algoritmos de baja precisión de D. Savoie (en todo caso no inferior a 0.05 grados), ya que los cálculos se repiten constantemente, si fuera necesaria más exactitud se recomienda consultar el calculador solar de la NOAA o similar.
Descripción de los items de la tabla
- Hora oficial(1) – Es la hora que marcan nuestros relojes (el reloj de pulsera, del PC, etc.). En la España peninsular la diferencia con respecto a la hora UTC es de una hora de adelanto (o de dos en el horario de verano). Esta hora es la utilizada como referencia en las otras horas de la tabla anterior. [La Hora legal suele ser la que corresponde al “huso horario” en que se encuentre la mayor parte del país, para el caso de la España peninsular es el UTC+0 coincidente con la hora UTC, la Hora oficial (que determina el gobierno) añade una hora (o dos en el horario de verano) a la Hora legal.]
- Hora UTC - Es la Hora Universal Coordinada, sustituye a la anteriormente denominada Hora media de Greenwich (GMT) u Hora civil de Greenwich (la precisión de la primera controlada mediante relojes atómicos, la de la segunda por el valor medio del día solar).
- Hora civil (o solar media contada desde medianoche) - Es la hora media anual (día = 86 400 s) referida al meridiano del lugar. Se utiliza frecuentemente en los anuarios astronómicos para especificar efemérides. La Horas civiles de La Coruña (8,4º O) y de Gerona (2,8º E) difieren 45 minutos, sus Horas legales y oficiales son las mismas. A esta hora solar media se le hace corresponder un sol medio o sol ficticio que se mueve a velocidad constante lo largo del año y que recorre el ecuador celeste (plano cuyos polos y ecuador son la proyección de los polos y ecuador terrestre), es decir, con una velocidad radial constante.
- Hora solar (solar verdadera, común, astronómica o equinoccial) - Es la hora real (no la media anual como lo son las horas anteriores: oficial, legal, UTC y civil), es decir, son las 12 del mediodía cuando el Sol cruza el meridiano del lugar (está en el punto más alto en el día), encara directamente al sur (hemisferio norte). Es la hora que marca un reloj de sol. Esta Hora solar no coincide, excepto cuatro días al año, con la Hora civil (que es una media), debido a la variación en la duración de los días en el ciclo de un año. Variación que puede llegar a ser de hasta 30 segundos diarios en relación con las 24 horas exactas y que al acumularse, se plasman en una diferencia horaria máxima de unos 16 minutos a principios de noviembre. Ver item 14 y la gráfica de la ecuación del tiempo a continuación de estos items. Esta hora solar verdadera refleja el movimiento del Sol real que recorre la eclíptica a lo largo del año con una velocidad radial variable y cuyo plano está inclinado 23,44º con respecto al plano ecuatorial celeste (véase definición del sol medio en el item anterior).
- Hora sidérea - Es el tiempo transcurrido desde la última vez en que un punto del cielo llamado Primer Punto de Aries pasó por encima de nuestro meridiano. Al tomar como referencia las estrellas y no al Sol, los días y horas sidéreos son ligeramente (~1/365) más cortos que los días y horas solares (unos 4 minutos menos que corresponden aprox. a 1 grado en la traslación terrestre). Se define como el ángulo horario del Punto Vernal, relacionada con la Ascensión recta (ver su definición más adelante).
- Hora itálica - Es el tiempo transcurrido desde el último atardecer. Si se resta de 24 nos da el tiempo que falta para que se ponga el Sol.
- Hora babilónica (o griega) - Es el tiempo transcurrido desde el último amanecer.
- Hora temporaria (desigual(2), planetaria(3), histórica o antigua) - Resulta de dividir el tiempo de iluminación en doce horas iguales entre sí y el tiempo de oscuridad en otras doce horas iguales entre sí. La duración de una hora temporaria varía dependiendo del día del año y también según ésta sea nocturna o diurna. Lo contrario a la hora temporaria o desigual es la hora igual, con ciclos de horas todas ellas iguales (la actual hora solar, las horas civil, UTC y oficial, así como las horas itálicas, babilónicas y sidéreas).
- Hora canónica - Su nombre proviene del uso en Europa durante la Edad Media para determinar las horas de los oficios religiosos en los monasterios. La hora es la que marca un reloj de sol vertical orientado hacia el sur con el gnomon perpendicular y con las líneas horarias equiespaciadas (segmentos equiangulares), horas que en sentido estricto deberían ser temporarias(4). En la tabla anterior se ha segmentado equiangularmente el día en 12 partes y la noche en 4 (vesperae, completa, matinae y laudes).
- Declinación - Es la latitud (positiva al Norte) del lugar de la Tierra donde el Sol se encuentra exactamente en el cenit.
- Longitud geográfica - Es la longitud (negativa al Oeste) del lugar de la Tierra donde el Sol se encuentra exactamente en el cenit.
- Longitud eclíptica - Es la distancia angular, tomando el Sol como centro, que hay entre el punto en que se encuentra actualmente la Tierra sobre su órbita y el punto en que se encontraba al entrar la primavera boreal (Punto Vernal).
- Ascensión recta - Es la proyección sobre el plano ecuatorial de la longitud eclíptica. Por motivos prácticos se mide en horas, pues también indica el tiempo sidéreo que lleva el Sol de retraso respecto al Punto Vernal. La ascensión recta (α) se relaciona con la hora sidérea (θ) y el ángulo horario del lugar (AH) de acuerdo con la ecuación: α = θ local - AH local.
- Ecuación del tiempo (EdT) - Es la diferencia entre la hora de un reloj de sol y la marcada por un reloj mecánico corregido en longitud y sin adelantos de hora o, lo que es lo mismo, el tiempo que hay que añadir a la Hora civil para que nos muestre la del reloj de sol. Esta cantidad varía según la época del año. Se mide como el adelanto del Sol sobre las 12:00:00 h a su paso por el meridiano de referencia. Ver gráfico más adelante.
- Elevación - Es la altura que tiene el Sol sobre el horizonte, medida en grados.
- Acimut - Es la dirección horizontal sobre la que se encuentra el Sol. Se mide en grados desde el Sur hacia el Oeste en el Hemisferio Norte y desde el Norte hacia el Este en el Hemisferio Sur.
- Máxima elevación - Es la mayor altura que alcanza hoy el Sol, medida en grados.
- Orto - Es el instante en que el centro del Sol asciende sobre horizonte. No confundir con el orto aparente.
- Mediodía - Es el instante en que el centro del Sol pasa por encima de nuestro meridiano. Coincide casi exactamente con el momento en que alcanza su máxima elevación.
- Ocaso - Es el instante en que el centro del Sol se oculta bajo el horizonte. No confundir con el ocaso aparente.
- Acimut al ocaso - Es la dirección horizontal del punto en que se pone hoy el Sol.
- Periodo de insolación - Es el tiempo que transcurre desde que amanece hasta que anochece en el día actual.
- Fecha gregoriana(5) - Es la fecha actual según el calendario gregoriano, oficial en España desde 1582. En la tabla la fecha viene indicada según la ISO-8601 (año-mes-día).
- Día juliano - Es la cantidad de días transcurridos desde el mediodía UTC del día uno de enero del año 4173 a.C. Se utiliza mucho al realizar cálculos astronómicos. Al comenzar la cuenta al mediodía del año mencionado, un día cualquiera viene indicado como un entero + 1/2, por ejemplo, el 1 de enero de 2020 como 2458849.5, momento en que termina el día. No tiene ninguna relación con los calendarios juliano o gregoriano.
Relación matemática entre Hora solar, Hora civil, Hora oficial y Ecuación del Tiempo (EdT)
La EdT, definida anteriormente, no es una "ecuación" al uso (matemático) y se la conoce con ese nombre desde hace siglos, entiéndase "ecuación" (del latín "aequatio") por "corrección" (su acepción astronómica en el diccionario de la RAE), que es lo que hace al corregir algebraicamente la hora solar media para obtener la hora solar verdadera.
Hora solar = Hora civil + EdT
Hora civil = Hora solar - EdT
O lo que es lo mismo y bastante usual, sustituyendo los nombres por equivalentes y poniendo la EdT de la ecuación a la izquierda:
EdT = Hora solar - Hora civil
EdT = Hora solar verdadera - Hora solar media
EdT = sol verdadero - sol medio o sol ficticio
EdT = tiempo solar verdadero - tiempo solar medio
EdT = tiempo aparente local (TAL) - tiempo medio local (TML)
EoT = local apparent time (LAT) - local mean time (LMT) -inglés-
Zeitgleichung (ZG) = ware ortszeit (WOZ) - mittiere ortszeit (MOZ) -alemán-
...
En España peninsular (la Hora oficial con 1 ó 2 horas de adelanto, corrección meridiano: 0 en 0º de longitud):
Hora oficial = Hora civil +- corrección meridiano + 1 ó 2
Hora civil = Hora oficial -+ corrección meridiano - 1 ó 2
Hora solar = Hora oficial + EdT -+ corrección meridiano - 1 ó 2
Hora oficial = Hora solar - EdT +- corrección meridiano + 1 ó 2
Nota: La EdT también suele definirse a la inversa, es decir, como el valor solar medio menos el verdadero (cambia el signo de la EdT).
En este caso, el gráfico de la ecuación del tiempo se mostrará invertido y los valores de la EdT en las tablas tendrán el signo cambiado. Recuérdese, para saber qué ecuaciones utilizar con la EdT, que el Sol (y el reloj) está retrasado a principios de año (Hora solar < Hora civil).
Excentricidad, oblicuidad y ángulo entre la líneas de solsticios y de ápsides (longitud del perihelio)
Planos de la eclíptica y del ecuador celeste, modelo geocéntrico.
Ambos forman un ángulo de 23,44º y se cortan en los equinoccios.
En la figura, al frente el equinoccio vernal o de primavera, oculto por
la Tierra el equinoccio de otoño, a la izda. y a la dcha. los solsticios
de invierno y de verano. El perihelio ligeramente a la dcha. del solsticio
de invierno y hacia el frente, el afelio en el lado opuesto. (fuente NASA)
El Sol, los planetas y las constelaciones del zodíaco se encuentran en el plano de la eclíptica. Se define como oblicuidad o inclinación axial de la eclíptica al ángulo que forman los ejes de rotación y de traslación terrestres, es decir, al ángulo que forma su plano ecuatorial con su plano orbital. Actualmente ese ángulo es de 23,44º (6) y se corresponde con el máximo y el mínimo de declinación solar.
Los tres factores físicos que intervienen en la ecuación del tiempo (EdT) y en el analema terrestre son:
1. Excentricidad
-
La velocidad en la órbita elíptica varía de acuerdo con la segunda ley de Kepler (en tiempos iguales, las áreas barridas por el planeta son iguales), es decir, cuando la Tierra está más alejada del Sol (afelio) su velocidad es menor que cuando está más cerca (perihelio), algo que dejó claro Newton con su ley de Gravitación Universal.
Debido a la excentricidad se realiza un ciclo de retraso-y-adelanto al cabo de un año.
2. Oblicuidad o inclinación axial
-
Y sí, además de afectar al distinto asoleamiento anual (las 4 estaciones), la inclinación del eje terrestre también provoca una variación en la hora solar con respecto a la hora solar media.
En este caso no es necesario recurrir a ninguna ley como en el anterior, es una simple cuestión geométrica. Consideremos que la órbita de la Tierra fuera circular. El sol medio o ficticio recorre el plano del ecuador celeste y el sol real el de la eclíptica, ambos parten del equinoccio de primavera simultáneamente a una velocidad constante, si proyectamos el sol real sobre el ecuador celeste, inicialmente su proyección estará retrasada con respecto al sol ficticio, la separación llegará a un máximo en el solsticio de verano y a partir de entonces la diferencia comenzará a disminuir hasta que ambos coinciden en el equinoccio de otoño, a continuación se vuelve a repetir lo anterior con otro máximo en el solsticio de invierno hasta llegar juntos al solsticio de primavera (punto de salida). Es precisamente en el ecuador celeste en donde se toma la referencia de tiempos, en donde transita el reloj medio o ficticio.
Debido a la inclinación se realizan dos ciclos de retraso-y-adelanto al cabo de un año.
3. Ángulo entre la línea de solsticios y la línea de ápsides (línea que une el perihelio y el afelio) o longitud del perihelio.
- Este ángulo no añade o resta tiempo a la hora solar, determina como se combinan las variaciones aportadas por la excentricidad y la inclinación axial(7).
Debido a la naturaleza dinámica de nuestro sistema solar estos tres items al cabo de los años y los siglos van cambiando, se conocen varios ciclos de entre los cuales es interesante mencionar:
- excentricidad, variación de 0,000055 a 0,0679, actualmente de 0,017 y decreciendo, ciclo de 413.000 años junto con otros ciclos de 95.000 y 125.000
- oblicuidad, variación de 22,1º a 24,5º, actualmente de 23,44º y decreciendo (22,43º en 2033), ciclo de 41.000 años, mínimo en torno al año 11.800. Añádasele un ciclo de corta duración (de 18, 8 años) debido a la "nutación de la Tierra", oscilación con una amplitud de 9,2 segundos de grado
- precesión axial o precesión de los equinoccios debido a las fuerzas de marea del Sol y de la Luna, actualmente el perihelio en verano en el hemisferio sur (máxima radiación), ciclo de 25.800 años
- precesión apsidal o precesión de la órbita eclíptica, ciclo de 112.000 años
Gráfico de la Ecuación del Tiempo (EdT)
La EdT puede mostrarse como parte del gráfico del analema poniéndola en su eje horizontal (componente este-oeste), o por sí sola para ver su evolución en el tiempo. Si se muestra por separado lo habitual es poner en el eje "x" (horizontal o transversal) los días del año y en el eje "y" (vertical o axial) la EdT (el adelanto o retraso del sol u hora solar con respecto a su valor medio anual).
Ecuación del Tiempo. Suma de los efectos de la excentricidad "en azul"
y de la inclinación "en rojo".
En el eje horizontal ("y" = 0) la hora solar media, en donde transita
el sol medio.
En la imagen se indican: P (perihelio), A (Afelio), EP (equinoccio
de primavera), SV (solsticio de verano), EO (equinoccio de otoño) y
SI (solsticio de invierno).
El efecto de la excentricidad y la inclinación son similares, el máximo
de una es aprox. 10 minutos y el de la otra de unos 8 minutos. (datos 2020, fuente NOAA)
La diferencia entre el tiempo solar verdadero y el tiempo solar medio varía, aproximadamente, entre los -14 minutos (hacia el 12 de febrero) y los 16,5 minutos (hacia el 4 de noviembre). Éstos son iguales en cuatro fechas (hacia el 15 de abril, el 13 de junio, el 1 de septiembre y el 25 de diciembre). Entre abril y mediados de septiembre, la diferencia suele ser de unos 3 minutos de media, una cantidad "permisible" si no se tiene en cuenta en la conversión de hora solar a hora oficial (máximo -7 minutos a finales de julio). La diferencia diaria varía, aproximadamente, entre los -30 segundos (hacia el solsticio de invierno) y los 22,5 segundos (hacia el equinoccio de septiembre)(8).
Se publican tablas anualmente con los valores de la EdT a lo largo del año (por ejemplo, en el Anuario del Real Observatorio de Madrid). Su variabilidad más notoria es debida a la existencia de un año bisiesto cada 4 años (calendario gregoriano), pocos segundos hay de diferencia entre una fecha determinada y la misma 4 años más tarde.
En el siguiente gráfico se muestra la EdT de forma poco habitual. Se han realizado los siguientes cambios con respecto al gráfico anterior: 1) intercambio de los ejes poniendo la EdT en el eje "x"; 2) el eje "y" de tiempos se ha cambiado de acuerdo con la figura de la izda. con las siguientes implicaciones: 2-a) cada número en el eje corresponde a 3,9 días, 23,44 a 3 meses; 2-b) se "duplica" el tamaño del eje transitándolo dos veces, del solsticio de verano (SV) al solsticio de invierno (SI) se invierte el recorrido teniéndose que contar desde el SV y añadir el valor de éste (44,3).
El motivo de estos raros cambios está claro, se trata de facilitar la comparación del gráfico de la EdT con el gráfico del analema que se verá más adelante (en donde está incluida). Nótese cómo se ha duplicado la distancia en los ciclos de las "sinusoides" de la inclinación y de la excentricidad, así como la distancia entre SI y SV. Cuando se sustituya el eje Y por una sinusoide (declinación solar) se completará la transformación, más evidente en los solsticios.
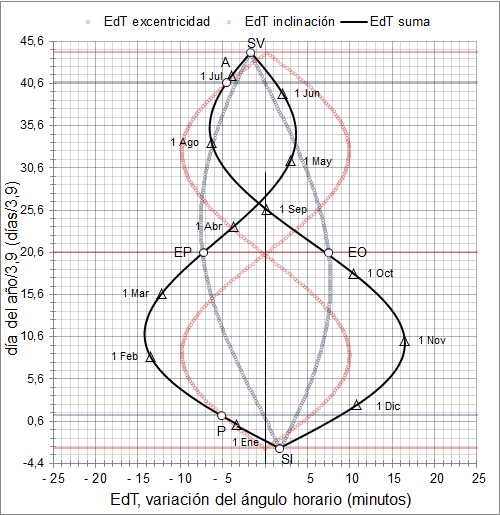
Ecuación del Tiempo, gráfico de transición. Suma de los efectos de la
excentricidad "en azul" y de la inclinación "en rojo". (datos 2020, fuente NOAA)
Gráfico del analema solar
Analema solar. Suma de los efectos de la excentricidad "en azul"
y de la inclinación "en rojo".
En el eje vertical ("x" = 0) la hora solar media, en donde transita
el sol medio.
Respecto al analema real, deformación en 2D por las coordenadas
ecuatoriales y por los ejes a distinta escala (x E. 4:1). (datos 2020,
fuente NOAA)
El gráfico de la EdT muestra el retraso y adelanto del sol en su recorrido diario anual. Otro gráfico útil es el que nos indica la distinta altura del Sol a determinadas horas debido a su declinación a lo largo del año (más elevada en los meses estivales que en los invernales para el hemisferio norte), es el gráfico de la declinación solar que se muestra junto a este párrafo (datos 2020, fuente NOAA).
Ambos gráficos tienen un eje de tiempo (días anuales transcurridos) lo que permite unirlos eliminando dicho eje. Poniendo la EdT (retraso y adelanto) en el eje horizontal y la altura debida a la declinación solar (que varía entre 23,44º a -23,44º) en el eje vertical, se obtiene una figura con la orientación y forma que tiene el analema solar en el firmamento (como era de esperarse).
Al haber eliminado el eje del tiempo, las fechas y la dirección del recorrido de la curva deben indicarse en la propia figura del analema, de no hacerse, el gráfico carecería de sentido si nos interesa saber el momento en que la EdT y la declinación tienen un determinado valor.
La falta de simetría en el analema respecto al eje vertical es debido a que no coinciden los solsticios con el perihelio y el afelio (diferencia de fase entre las dos curvas). Nótese en el gráfico que los valores que se han utilizado para los ejes varían entre 25 y -25, pero el eje de la declinación está en grados mientras que el eje de la EdT está en minutos, es decir, este último está a una escala 4 veces mayor (1 hora = 60 minutos = 15 grados). Se muestra el analema de esta manera ya que es conveniente ampliarlo para facilitar la visualización de los detalles de la figura, aunque el analema real que "dibuja" el Sol en el firmamento sea cuatro veces más estrecho, entre otras cosas(8).
El aporte de la excentricidad ("elipse") y el momento en que lo hace, desdibuja los bucles y altera la simetría de la curva de la inclinación ("lemniscata", o "lemniscata de Gerono" escalando los ejes) del analema. Ninguna de ellas desaparecerá de acuerdo con los ciclos de máximos y mínimos que se ha visto anteriormente. Con el paso de unos cuantos miles de años en el analema se alternará el tamaño de los bucles inferior y superior al igual que su asimetría respecto a los ejes. Dados los valores de la inclinación, para que desaparezca uno de los bucles, la excentricidad debe superar 0,04, actualmente es de 0,017 y disminuyendo (larga espera).
Como referencia de la EdT se pueden utilizar tanto el gráfico de la EdT como el del analema, éste último aporta información adicional de la declinación solar en el eje vertical perdiendo, por el cambio, la escala de tiempos del primero. Además de los gráficos, también se publican tablas con la EdT (véase documento adjunto al final de esta página) y con la declinación solar a lo largo de todo un año o con valores medios plurianuales.
Hay que tener cautela y no identificar la figura del analema en un gráfico con la real, salvo en determinados casos en que esa imagen se haya creado intencionadamente (y así se diga), por ejemplo, en las figuras del analema en los gráficos con fondo azul que se muestran más adelante. Esta es una de las pocas ocasiones en que el análisis de algo puede confundirse con el sujeto de dicho análisis.
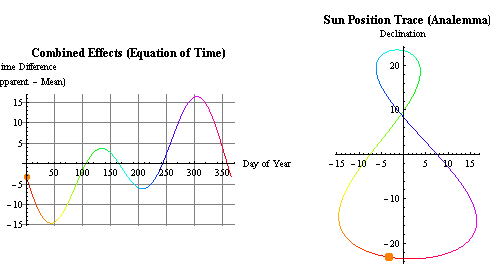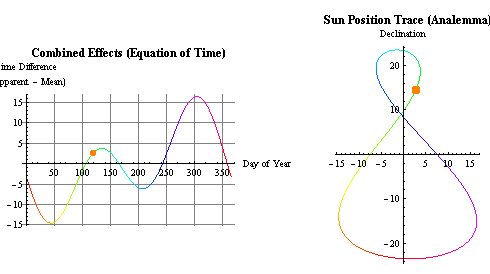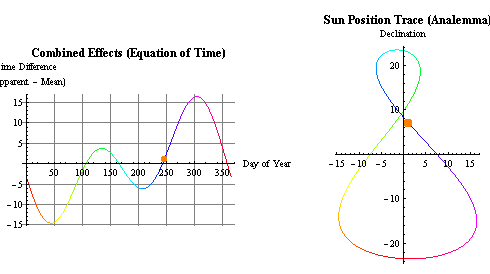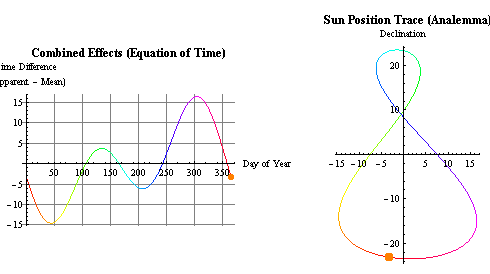
EdT y analema (deformación en 2D por las coordenadas ecuatoriales y los
ejes a distinta escala (x E. 4:1)). En la EdT el sol ficticio recorre el eje "x"
a velocidad constante. En el analema el sol ficticio recorre el eje "y" en
ambas direcciones a velocidad variable, ésta última afectada por las
variaciones de la declinación solar lo que justifica la etimología de la
palabra "solsticio" (solstitium, sol y estatum -estático-), variación mínima.
Analema solar
Simulación del analema solar en el Observatorio de Madrid
(latitud 40,408333º N) a las 9:00 Hora civil, con soles a escala
cada 7 días. Inclinado -39,71311º al no ser mediodía. (datos 2020,
fuente NASA/JPL/Horizons)
Como ya se ha visto, el analema solar es una curva con forma similar a la de un 8 con ejes de tiempo y de declinación solar, la prueba de ello nos la da el propio Sol si se fija su posición en el cielo durante todos los días del año observándolo a la misma Hora civil desde un mismo lugar. Dependiendo de la hora elegida y de la latitud del lugar su inclinación variará, será vertical a las 12:00 Hora civil. También se puede ver el analema solar indirectamente, con la sombra del sol en los relojes solares (en donde inicialmente apareció su figura)10 o sobre cualquier superficie plana. Además del analema solar hay muchos otros analemas (de cuerpos que aparente o realmente giran alrededor de otro) y algunos con formas peculiares interesantes.
Simulación de un ciclo de analemas solares en cualquier punto
terrestre a las 12:00 Hora civil (mediodía). Fechas: "en azul" 4080 a. C.,
"en blanco" 1247, "en amarillo" 2020, "en naranja" 6426 y "en violeta"
aprox. 11480.
Se indica en grados la posición del perihelio respecto al equinoccio de
primavera, tanto la excentricidad como la inclinación van disminuyendo
(fuente datos NASA/JPL/Horizons y Meeus, cálculos imprecisos dadas las fechas)
Variación del analema terrestre debido a la excentricidad, oblicuidad y
longitud del perihelio. "En rojo" año 2023 (e=0,016694, ε=23.4368 y λp=283.290)
Datos del simulador del Goddard Institute (NASA)
Gráficos, Sundial Atlas (Fabio Savian). Composición, AARS (Luis E. Vadillo)
En el gráfico anterior se aprecia mejor la lenta variación del analema (y de la Ecuación del Tiempo) con el paso de los años. Se han elegido 5 fechas en que la longitud del perihelio sea 90º o múltiplo de la misma (1246, 6446, 11513, 16656 y 21183 -años que difieren ligeramente de los obtenidos con el simulador de JPL/NASA en otra imagen anterior-); no tiene inclinación a 270º y 90º, inclinado a la dcha. a 0º e inclinado a la izda. a 180º. Nótese que su forma también cambia a lo largo de estos aprox. 20.000 años. Al comparar las fechas 1246 y 21183 con idéntica longitud del perihelio, son distintos los valores de la excentricidad (35 % de 0,017, casi circular) y de la oblicuidad (98% de 23,5376º). El año 2023 se ha añadido en rojo, tiene una pequeña inclinación inexistente en 1246 (año en que coincidió el perihelio con el solsticio de invierno).
---
(1) Ya en el siglo XVIII los relojes mecánicos son bastante exactos marcando 24 horas al día, su coexistencia con los relojes de sol puso de manifiesto a las gentes que la hora de ambos no era igual, pues esto obligaba a corregirlos constantemente para que coincidiera el mediodía marcado por los relojes de sol con las 12 horas de su dial, es decir, forzándolos a mostrar el tiempo verdadero de los solares (tiempo que es distinto a 24 horas al día a lo largo del año, 24 horas al día es su media anual). El "problema" se resolvió utilizando una tabla conocida por los astrónomos y relojeros como la "ecuación del tiempo" , que cuantifica la diferencia entre ambas horas durante todo el año. De forma que, ajustando la hora de los relojes mecánicos con los relojes de sol teniendo en cuenta dicha diferencia, según la fecha y de acuerdo con la tabla, éstos mostrarán el tiempo medio (24 horas todos los días del año) y no el tiempo verdadero. Un reloj mecánico que no se atrase ni se adelante, no necesita ajuste.
No solo era la exactitud sino, también, la proliferaciòn de relojes mecánicos lo que obligaba a utilizar el tiempo medio. Un período de cambio en el que buena parte de la población no quería abandonar el tiempo usado anteriormente. Ambos tiempos eran conocidos por muchos, algo que hoy día lo es por pocos (ver Semanario Pintoresco Español 40, Tomo II de 1837 en adjuntos).
El paso de tiempo verdadero a tiempo medio supuso un cambio radical. El tiempo verdadero que está vinculado a la posición del sol, se reemplaza por un tiempo medio que es una abstracción matemática que lo desconecta de la realidad física. Es la primera de varias uniformizaciones que se harán de la medida del tiempo. La hora solar se reemplaza por la hora civil.
Oficialmente, el abandono del tiempo verdadero (relojes de sol) y paso al tiempo medio en los relojes mecánicos se realiza en Europa a partir de finales del siglo XVIII. En España se va adoptando por las distintas poblaciones en sus relojes públicos hacia mediados del siglo XIX con amplia difusión de la tabla de la "ecuación del tiempo" (ver Gaceta de 4287 de 1846 en adjuntos). En la provincia de Madrid se publica la orden para el ajuste de los relojes mecánicos públicos a tiempo medio mediante la tabla mencionada el 23 de junio de 1846 (ver Boletín de Madrid 2487 de 1846 en adjuntos).
Tabla para el arreglo de los relojes - Boletín de Madrid 2487 de 1846
Eje X, unidades de 5 días (73 al año). Eje Y, minutos de adelanto o de retraso
de reloj con tiempo medio. En negro datos del boletín, en rojo EdT de 2022 (ambos valores similares)
La necesidad creciente de tener un primer meridiano y una hora común para todo el Estado aún quedaba por resolver. Por ejemplo, para los trabajos astronómicos y geográficos, el 1 de mayo de 1869 se crea una comisión encargada de elegir entre los meridianos de Madrid y el de San Fernando (Cádiz) "para todos los trabajos que se ejecuten o publiquen por cuenta del Estado" (ver Gaceta 121 de 1869 en adjuntos), nunca se llegó a elegir. Por ello, la inexistencia de un tiempo medio para ese meridiano impedía tener una hora de referencia para todo el Estado. Aunque, de facto, se siguieron utilizando ambos meridianos y como hora común la del Observatorio de Madrid, que solía indicarse como "tiempo medio de Madrid".
Antes de 1901 las distintas poblaciones tenían sus propias horas locales. Eso suponía, por ejemplo, una hora de diferencia entre Barcelona y La Coruña, un problema para el servicio de ferrocarriles, correos, telegrafía, así como para los Ministerios, Tribunales y oficinas públicas, etc. Por lo anterior, se decide adoptar en toda España, a partir de la 0 horas del 1 de enero de 1901, el tiempo solar medio del meridiano de Greenwich (GMT) conocido como "tiempo de la Europa occidental" (ver Gaceta 209 de 1900 en adjuntos).
El 16 de marzo de 1940 a las 23 horas se adopta como hora oficial la UTC+1 (se adelanta una hora), "considerando la conveniencia de que el horario nacional marche de acuerdo con los de otros países europeos, y las ventajas de diversas órdenes que el adelanto temporal de la hora trae consigo". Es decir, se pasa de la zona horaria de Europa occidental (WET) a la zona horaria de la Europa Central (CET) (ver BOE 68 de 1940 en adjuntos).
El 15 de abril de 1918 se introduce por primera vez el horario de verano (adelanto de una hora), "como medio de conseguir el ahorro de carbón", horario que se ha utilizado desde entonces intermitentemente. Entre 1950 y 1973 esa práctica se abandonó por completo, retomándose en 1974 debido a la crisis del petróleo de ese año (ver Gaceta 94 de 1918 y "Horario de verano BOE-A-2022-2026" en adjuntos).
(2) La hora desigual es sinónima de hora temporaria siempre y cuando no se considere la existencia de otro tipo de hora desigual. Esta equivalencia desaparece al añadir, por ejemplo, la hora planetaria definida como segmento de la eclíptica (ver (3)). Se puede redefinir la hora desigual opuesta a la hora igual y característica de las horas temporarias, planetarias, etc. Los distintos tipos de horas atendiendo a su duración pueden esquematizarse de la siguiente forma:
Iguales
- - hora solar verdadera (y civil, UTC, oficial)
- - hora babilónica
- - hora itálica
- - hora sidérea, raro uso en relojes de sol
Desiguales
- - hora temporaria. 12 horas diurnas e iguales entre sí
- - hora planetaria. 12 horas diurnas y desiguales entre sí. Definida como segmento de la eclíptica (ver (3)), raro uso en relojes de sol
- - hora equiangular. Horas desiguales entre sí. Sin definición, igual separación angular entre horas en los relojes de sol. Entre otros, utilizada en el diseño por la mayoría de relojes verticales meridionales de horas canónicas (ver (4))
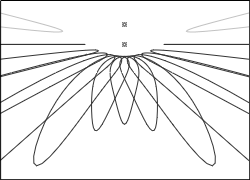(3) Hora planetaria. Con el mismo adjetivo existe documentación para dos tipos de horas:
1. Definida antiguamente como el tiempo requerido para el orto de 15º de la eclíptica contándose desde la salida del sol.
Dado que en el orto la eclíptica va variando con el tiempo en inclinación y distancia del ecuador celeste, las horas planetarias son desiguales entre si a lo largo del día así como entre un día y el siguiente. Hay 12 horas planetarias entre el orto y el ocaso y otras 12 horas nocturnas. En la imagen de la izda. puede verse el trazado de horas planetarias en un reloj de sol vertical meridional (latitud 40º).
2. A partir del Renacimiento se suele utilizar la misma denominación de hora planetaria al referirse a las horas temporarias, entre otros motivos, para diferenciarlas de las horas solares verdaderas o comunes (estas últimas introducidas en Europa a partir del siglo XIV) y de las equiangulares.
(4) En Europa durante la Edad Media, en vez de utilizarse el trazado de las horas temporarias heredadas de la Edad Antigua en los relojes de sol verticales orientados al sur, de forma heterodoxa lo simplifican con la simple división en partes iguales entre sí en la cara del reloj (horas equiangulares). Es más, de las doce partes del día y para indicar la hora de los oficios religiosos en monasterios y conventos solo se solían trazar las líneas que corresponden a prima, tercia, sexta, nona y vísperas (agrupación de horas), nomenclatura que da origen a las llamadas horas canónicas. Estos relojes de sol se realizaban en muros con un gnomon perpendicular y con forma circular o semicircular, muchos de ellos toscamente grabados.
Los cambios estacionales afectan bastante a las horas temporarias y canónicas, en algunas órdenes monásticas se establecieron distintos horarios para sus actividades según la época del año. En partes de Europa el horario fue adelantándose poco a poco en la última mitad de la Edad media, llegándose a realizar al mediodía los rituales de la hora nona ("noon" en inglés).
Si bien se pueden trazar horas temporarias en un reloj horizontal, no puede hacerse un reloj horizontal canónico con un trazado equiangular, necesariamente hay que utilizar, de forma ortodoxa, horas temporarias. Lo mismo para el caso de relojes verticales no orientados al sur.
En la parte superior de la siguiente figura puede verse la comparación de los trazados de un reloj vertical meridional para una latitud de 30º N, la diferencia entre las horas es mayor cuanto mayor sea la latitud. El gnomon (varilla) es perpendicular a la cara del reloj para las horas temporarias y equiangulares, y paralelo al eje terrestre para las horas solares. También se muestra en la parte inferior un reloj horizontal con trazado equiangular inválido.
Trazado de reloj vertical meridional y reloj horizontal para latitud
30º N con horas temporarias "en negro", equiangulares 15º "en rojo" y
solares "en azul" (equiangulares 15º similares a temporarias en el
vertical, inválidas en el horizontal)
Trazado de reloj vertical meridional para latitud 46º N con horas
temporarias agrupadas como canónicas (diseño de Mauro Giongo, 2021)
(5) El cómputo en la era cristiana se cambió de calendario juliano a calendario gregoriano por el papa Gregorio XIII para corregir un error del primero, al jueves 4 de octubre de 1582 juliano le sucede el 15 de octubre gregoriano (10 días más). Por desgracia, se realizó en dicha fecha solo en Italia, Portugal, España y parte de Polonia. Posteriormente lo fueron adoptando otros países, Francia, Países Bajos y Bélgica el mismo año, Alemania y Austria al siguiente, otros muy distanciados en el tiempo, p.ej.: Inglaterra en 1752 (11 días más), Rusia en 1918 (13 días más), etc.
En España también se utilizó la era hispánica o de Augusto hasta el siglo XIV/XV, ésta se inicia 38 años antes que la cristiana. Se indica con el ordinal precedido de "era".
(6) Variación de la OBLICUIDAD. La posición de los trópicos de Cáncer y de Capricornio, y de los círculos polares Ártico y Antártico, dependen de la inclinación del eje de la Tierra con respecto a plano de su órbita alrededor del Sol. Este ángulo no es constante y viene determinado por la superposición de ciclos de duración variable. La variación a largo plazo de éste ángulo fluctúa entre aproximadamente 22,1º y 24.5º con una periodicidad de unos 41.000 años.
Trópico de Cáncer en CF 83 (Tamaulipas, México), años 2005-2010 con marcas espaciadas
en dirección N-S (fotografía de Wkboonec, CC SA), actualmente desaparecidas
En 2023,5 la inclinación es de 23,43623618º (23º 26' 10,45'') y su medida disminuye aproximadamente 0,4681 segundos de grado por año (0,00013º por año), es decir, una centésima de grado cada 76,91 años. En enero de 2033 su redondeo a dos decimales pasará de 23,44º a 23,43º (23º 26' 5,99''). En octubre de 2045 será de 23º 26', un minuto menos que en 1917 (128 años antes). Esta variación de la inclinación causa que los trópicos se acerquen al ecuador y los círculos polares a los polos del orden de 14,447 m por año (1 km cada 69,218 años). Cálculos anteriores de acuerdo con J. Laskar, Astronomy and Astrophysics vol 157, pp 68-69, 1986, y una circunferencia terrestre de 40 Mm.
La "nutación de la Tierra" es un ciclo de 18,6 años de duración y afecta a la oblicuidad a corto plazo, tiene una amplitud de unos 300 metros (9,2 segundos), llegando a ser la diferencia máxima anual de unos 3 segundos, que si se suman a los 0,47 segundos del párrafo anterior, la diferencia anual en los trópicos y círculos polares supera los 100 m.
En la figura anterior (diseño de H. Sulzer, CC Share Alike) pueden verse tres movimientos terrestres: [R] rotación sobre su eje (ciclo de 24 horas), [N] nutación (ciclo de 18,6 años) y [P] precesión de los equinoccios (ciclo de aprox. 25.800 años, 1 día de adelanto en el calendario anual cada 70,7 años).
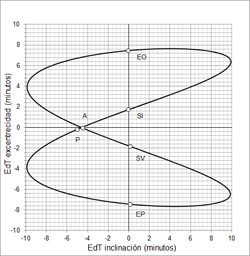
(7) El gráfico (datos 2020, fuente NOAA) nos muestra la relación entre la inclinación del eje terrestre y la excentricidad actualmente (faltan por incluir las fechas de forma similar a como se ha hecho en el gráfico del analema). La figura resultante varía bastante dependiendo del desfase entre ambas curvas, una con período el doble que la otra. Es similar a una de las curvas de Lissajous del tipo (2:1):
x = A * sen(2t + desfase), y = B * sen(t); con un desfase de 90º
En la imagen de la izquierda puede verse como varía la figura variando el desfase entre las 2 sinusoides. En la Tierra se nota ese cambio con el paso de los siglos, en 1246 d.C. el solsticio de invierno y el perihelio terrestre coincidían, por ello, el analema era simétrico respecto al eje vertical, el gráfico de la excentricidad y la inclinación formaba una "lemniscata", o "lemniscata de Gerono" escalando los ejes.
Este es un gráfico que no se suele utilizar ya que hay poco interés en saber qué parte de la corrección horaria se debe a la excentricidad y qué parte a la inclinación del eje y eso, también, se puede observar en el gráfico de la EdT añadiendo la excentricidad y declinación por separado como se muestra en esta página.
(8) Al gráfico de la EdT (en minutos) se le ha suprimido el trazado de sus componentes (excentricidad e inclinación) para una visualización más clara y se le añade la diferencia diaria o velocidad (en segundos) con que varía ésta. Es decir, para una determinada fecha, la curva en negro nos indica los minutos acumulados de retraso o adelanto de la hora solar y la curva en naranja los segundos que se le añaden o restan ese día. La diferencia diaria varía, aproximadamente, entre los -30 segundos (hacia el solsticio de invierno) y los 22,5 segundos (hacia el equinoccio de septiembre).
Los máximos y mínimos de la velocidad (curva naranja, variación diaria) coinciden con las mayores pendientes de la EdT (curva negra) y los valores nulos de la velocidad coinciden con máximos y mínimos de la EdT.
[De igual forma, se podría haber trazado en el gráfico una curva de aceleración (variación de la velocidad con respecto al tiempo), pero ello lo complicaría. Sin embargo, es fácil imáginárselo: las máximas y mínimas acelaciones coincidirían con las mayores pendientes de la velocidad y los valores nulos de la aceleración coincidirían con los valores máximos y mínimos de la velocidad.]
Ecuación del Tiempo y velocidad
En el eje horizontal ("y" = 0) está la hora solar media
En el eje vertical, los minutos de retraso o adelanto de la hora solar (en negro)
y los segundos de retraso o adelanto del día (en naranja)
indican: P (perihelio), A (Afelio), EP (equinoccio
de primavera), SV (solsticio de verano), EO (equinoccio de otoño) y
SI (solsticio de invierno).
(9) Sabiendo que la rotación terrestre en un día son 360 grados y que ésta dura 24 horas, a cada hora le corresponden 360/24 = 15 grados. A la izda. de la imagen, forma habitual de presentar el analema para fines didácticos, la escala de eje vertical en grados y la del eje de la EdT en minutos, es decir, 4 veces mayor (1 hora = 60 minutos = 15 grados). A la dcha. el mismo analema reduciendo el eje horizontal a un cuarto para que ambos ejes tengan la misma escala, aspecto similar al analema que "dibuja" el sol en el firmamento (con deformación en 2D por las coordenadas ecuatoriales).
Analema a distintas escalas, ambas iguales a la dcha.
(10) Proyectando la sombra del Sol sobre un punto a una determinada distancia de una superficie a lo largo del año se dibujará una imagen del analema solar (proyección gnomónica). Esta imagen estará distorsionada dependiendo de como sea dicha superficie y de su orientación. Para el caso particular de un plano se obtienen imágenes como las que se muestran, la de la izda. en un plano vertical y la de la dcha. en un plano horizontal. Ambas de sendos relojes de sol para la latitud del meridiano de Madrid.
Un reloj de sol "puede" mostrar la hora oficial al igual que la solar verdadera y otras más. Pero si las distintas horas solares son rectas, las horas civiles y oficiales serán analemas, evidente (son horas medias). Es más, también puede verse en las imágenes que la sombra de un punto puede indicarnos la fecha gracias a la declinación solar, las curvas que cortan las horas, extremos de los analemas, nos muestran desde el solsticio de invierno (parte superior) al solsticio de verano (parte inferior) y viceversa, siendo los equinoccios la recta intermedia.
Nótese que la deformación del analema solar en ambos relojes es distinta debido a las inclinaciones de los mismos. El lóbulo superior del analema se proyecta en la parte inferior de los relojes, en el vertical se agranda y en el horizontal se empequeñece.
Relojes de sol para latitud 40,408333º N (Observatorio de Madrid). Izda. vertical y dcha. horizontal
Marcan la hora solar (rectas), hora civil (analemas) y fechas (hipérbolas y recta equinoccial)
El analema se deformará menos si el plano del reloj coincide con el eje norte-sur terrestre, aunque, como en los 2 relojes anteriores, los analemas de las horas distintas al mediodía seguirán engrosándose. Esto último puede evitarse si el reloj fuera cilíndrico como se muestra en las siguientes imágenes.
Reloj de sol polar cilíndrico monumental, hora oficial, analemas cada 15 minutos
Muelle viejo de Palma (Mallorca, España), diámetro 4,6 m, autor: Rafael Soler Gaya (1985)
Enlaces relacionados
Ecuación del tiempo en Wikipedia
Equinoccios, solsticios, perihelio y afelio
¿Dónde está el Sol (longitud y declinación)?
Efemérides anuales del Sol en Astropixels
Husos horarios en Wikipedia
Cambio de calendario Juliano a Gregoriano en Ancestor Check
---
Luis Eusebio Vadillo Sacristán - AARS
Original 2007-06-02. Última actualización 2024-04-04
| Adjunto | Tamaño |
|---|---|
| Semanario-Pintoresco-Esp-1837-n40-pp-401-403.pdf | 1.09 MB |
| Boletin-Mad-1846-n2487.pdf | 737.51 KB |
| Gaceta-Mad-1846-n4287.pdf | 1.88 MB |
| Gaceta-Mad-1869-n121.pdf | 5.73 MB |
| Gaceta-Mad-1900-n209.pdf | 8.53 MB |
| Gaceta-Mad-1918-n94.pdf | 6.39 MB |
| BOE-1940-n68.pdf | 3.87 MB |
| Se-mantiene-el-cambio-estacional-Moncloa-2019-03-22.PNG | 148.15 KB |
| Horario-de-verano-BOE-A-2022-2026.pdf | 194.05 KB |
| Equinoccios-y-Solsticios-2001-2100.pdf | 457.43 KB |
| CALENDARIO-2023-Reloj-Andalusi.pdf | 25.97 MB |
| CALENDARIO-2024-Reloj-Andalusi.pdf | 80.14 MB |
| Declination-at-0-meridian-2000-2100-Gnomoni-ca.png | 84.96 KB |
| EoT-2001-2400-ArsGnomonica-Sundial-Atlas.pdf | 358.71 KB |
| EoT-2020-illustratingshadows.com1_.pdf | 509.59 KB |
| EoT-2021-illustratingshadows.com1_.pdf | 82.27 KB |
| EoT-2022-illustratingshadows.com1_.pdf | 82.34 KB |
| EoT-2023-illustratingshadows.com1_.pdf | 82.33 KB |
| EoT-2024-illustratingshadows.com1_.pdf | 77.79 KB |
- 325165 lecturas